AI
데이터 분석 및 의미 찾기 1
0_hailey_0
2024. 2. 28. 17:07
<Chapter1. 가설 검정>
1. 가설과 가설 검정
*️⃣ 과학 연구 절차


1) 모집단(Population)
: 우리가 알고 싶은 대상 전체 영역(데이터)
2) 표본(Sample)
: 그 대상의 일부 영역(데이터)
=> 모집단을 대표할 수 있는지 알 수 있음! (진짜 알고 싶은 건 모집단)
✔️ 일부분으로 전체를 추정하고자 한다면
- 모집단에 대한 가설 수립
- 가설은 보통 x와 y의 관계를 표현
- X에 따라 Y가 차이가 있다.
- X와 Y는 관계가 있다.
- 가설은 보통 x와 y의 관계를 표현
- 표본을 가지고 가설이 진짜 그러한지 검증(검정)
<Chapter2. 이변량 분석 1 : 숫자 -> 숫자>
X와 Y의 관계가 강한지 약한지 알아보기 위해 도구를 이용한다!

1. 시각화: 산점도
- 상관 분석
- 상관 분석은 연속형 변수 X에 대한 연속형 변수 Y의 관계를 분석할 때 사용
- Scatter를 통해 시각화
- 가설 : 온도(x)가 상승하면 아이스크림 판매량(y)을 증가할까?
- 어떤 관계가 보이나요?
- 얼마나 강한 관계인가요?
- 숫자 vs 숫자를 비교할 때 중요한 관점이 '직선'(Linearity)
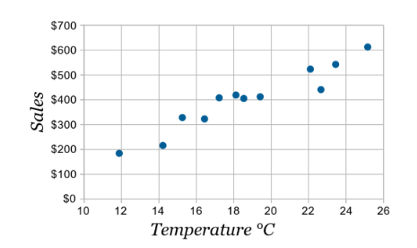
1) 산점도
- 문법
- plt.scatter( x축 값, y축 값 )
- plt.scatter( ‘x변수’, ‘y변수’, data = dataframe이름)
plt.scatter(air['Temp'], air['Ozone'])
plt.show()
plt.scatter(air['Temp'], air['Ozone'])
plt.show()
sns.scatterplot(x='Temp', y='Ozone', data = air)
plt.show()
#그래프 전체 크기
plt.figure(figsize = (12, 3))
#그래프 1행 3열로 그리기
plt.subplot(1, 3, 1)
sns.scatterplot(x='Temp', y='Ozone', data = air)
plt.grid()
plt.subplot(1, 3, 2)
sns.scatterplot(x='Wind', y='Ozone', data = air)
plt.grid()
plt.subplot(1, 3, 3)
sns.scatterplot(x='Solar.R', y='Ozone', data = air)
plt.grid()
plt.show()
- 두 변수의 관계
- 산점도에서 또렷한 패턴이 보인다면, 강한 관계
- 얼마나 직선에 모여 있는가 => 강한 관계
- 특히, 직선의 패턴이 보인다면
2) pairplot 한꺼번에 시각화
- 숫자형 변수들에 대한 산점도를 한꺼번에 그려줌.
- 그러나 시간이 많이걸림.
sns.pairplot(air)
plt.show()
3) jointplot, regplot
- jointplot은 산점도와 각각의 히스토그램을 함께 보여준다.
sns.jointplot(x='Solar.R', y='Ozone', data = air)
plt.show()
sns.regplot(x='Solar.R', y='Ozone', data = air)
plt.show()
2. 수치화: 상관분석
1) 상관계수, p-value
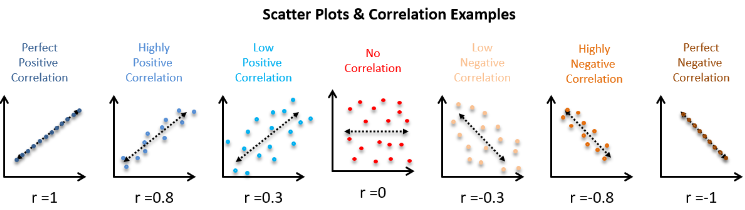
- 상관계수 𝑟
- 공분산을 표준화 한 값
- -1 ~ 1 사이의 값
- -1, 1에 가까울수록 강한 상관관계를 나타냄.
- 경험에 의한 대략의 기준(절대적인 기준이 절대 아닙니다.)
- 강한 : 0.5 < |𝑟| ≤ 1
- 중간 : 0.2 < |𝑟| ≤ 0.5
- 약한 : 0.1 < |𝑟| ≤ 0.2
- (거의) 없음 : |𝑟| ≤ 0.1
import scipy.stats as spst
# 상관계수와 p-value
spst.pearsonr(air['Temp'], air['Ozone'])
결과는 튜플로 나오는데
- 튜플의 첫 번째 값 : 상관계수
- 두 번째 값 : p-value
- 귀무가설 : 상관관계가 없다.(상관계수가 0이다.)
- 대립가설 : 상관 관계가 있다.(상관계수가 0이 아니다.)
- 주의 사항 : 값에 NaN이 있으면 계산되지 않음. 반드시. notnull()로 제외하고 수행!

2) 데이터프레임 한꺼번에 상관계수 구하기
- df.corr()
# 데이터프레임으로 부터 수치형 데이터에 대한 상관계수 구하기
air.corr()
위 결과로부터,
- 같은 변수끼리 구한 값 1은 의미 없다. 대각선은 보지 말기! ((2), (3))은 같은 값으로 한쪽만 보자!
- 상관계수의 절댓값이
- 1에 가까울수록 강한 상관관계
- 0에 가까울 수록 약한 상관관계
- 가장 강한 상관관계: Temp - Ozone : 0.683372
- 가장 약한 상관관계: Wind - Solar.R : -0.056792
- +는 양의 상관관계, -는 음의 상관관계
3) 상관계수를 heatmap으로 시각화
plt.figure(figsize = (8, 8))
sns.heatmap(air.corr(),
annot = True, # 숫자(상관계수) 표기 여부
fmt = '.3f', # 숫자 포멧 : 소수점 3자리까지 표기
cmap = 'RdYlBu_r', # 칼라맵
vmin = -1, vmax = 1) # 값의 최소, 최대값
plt.show()
빨간색에 가까울 수록 양의 상관관계, 파란색과 가까울 수록 음의 상관관계, 노란색은 관계없음.
4) NaN을 제외(.notnull())하고, 상관분석
air.isna().sum() # NaN을 찾는 방법temp = air.loc[air['Solar.R'].notnull()]
spst.pearsonr(temp['Solar.R'], temp['Ozone'])
<Chapter 4. 이변량분석: 범주 -> 숫자>
1. 시각화
1) 평균 비교: barplot
- 신뢰구간(오차범위)
- 평균값이 얼마나 믿을 만 한가?
- 좁을 수록 믿을 만 하다.
- 데이터가 많을수록, 편차가 적을 수록 신뢰구간은 좁아 짐.
- 두 평균에 차이가 크고, 신뢰구간은 겹치지 않을 때, 대립가설이 맞다고 볼 수 있다.
sns.barplot(x="Survived", y="Age", data=titanic)
plt.grid()
plt.show()
2. 수치화
1) t-test: 두 집단의 평균을 비교
- 두 그룹간 평균에 차이가 있는가?
- 그룹 A의 평균 vs. 그룹 B의 평균
- 범주의 수 2개 일 때 사용.
- t 통계량
- 두 평균의 차이를 표준오차로 나눈 값.
- 기본적으로는 두 평균의 차이.
- 우리의 가설(대립가설)은 차이가 있다는 것이므로, t 값이 크던지 작던지 하기를 기대.
- 보통, t 값이 -2보다 작거나, 2보다 크면 차이가 있다고 본다.
- ttest_ind(B, A, equal_var = False)
- A와 비교할 때 B의 평균이 큰가?
- equal_var :A와 B의 분산이 같은가? -> 모르면 False(default)
# 먼저 NaN이 있는지 확인해 봅시다.
titanic.isna().sum()
# NaN 행 제외
temp = titanic.loc[titanic['Age'].notnull()]
# 두 그룹으로 데이터 저장
died = temp.loc[temp['Survived']==0, 'Age']
survived = temp.loc[temp['Survived']==1, 'Age'
# t-test
spst.ttest_ind(died, survived)
2) anova
- 분산 분석 ANalysis Of VAriance
- 전체평균과 각 그룹 평균에 차이가 있는가?
- 범주의 수 3개 이상일 때 사용.
- 여기서 기준은 전체 평균.
- 𝐹 통계량 =
- (집단 간 분산)/(집단 내 분산) = (전체 평균 − 각 집단 평균)/(각 집단의 평균 − 개별 값)
- 값이 대략 2~3 이상이면 차이가 있다고 판단.
# Pclass(3 범주) --> Age
sns.barplot(x="Pclass", y="Age", data=titanic)
plt.grid()
plt.show()
# 1) 분산 분석을 위한 데이터 만들기
# NaN 행 제외
temp = titanic.loc[titanic['Age'].notnull()]
# 그룹별 저장
P_1 = temp.loc[temp.Pclass == 1, 'Age']
P_2 = temp.loc[temp.Pclass == 2, 'Age']
P_3 = temp.loc[temp.Pclass == 3, 'Age']
# 2) anova
spst.f_oneway(P_1, P_2, P_3)
[2주차 03]