데이터 처리 2
<Chapter 5.시각화 라이브러리>
1. 데이터의 시각화

2. matplotlib와 seaborn 패키지
: 파이썬의 시각화 패키지
3. 기본 코드 구조
1) matplotlib.pylot
- matplot.pyplot의 별칭으로 plt 사용
- Seaborn의 별칭은 sns
2) plt.plot()
- 기본 라인차트를 그려준다.
3) plt.show()
- 그래프를 화면에 출력
4. 기본 코드: x, y값 지정하기
1) x와 y값 지정
- 1차원 : list, numpy array, series 등을 각각 x와 y로 지정해서 사용
- 2차원 : dictionary, dataframe로 부터 x와 y를 가져와서 사용 가능
2) 문법
- plt.plot(x, y)
- plt.plot(x, y, data)
# 타입1
plt.plot(data['Date'], data['Temp'])
plt.show()
# 타입2
plt.plot('Date', 'Temp', data = data)
plt.show()
5. x축 값 기울기 조정하기
1) X축 값 조정하기
- plt.xticks(rotation = 각도)
2) 축 레이블 붙이기
- plt.xlabel(), plt.ylabel()
3) 그래프 타이틀 붙이기
- plt.title()
plt.plot(data['Date'], data['Ozone'])
plt.xticks(rotation = 30)
plt.xlabel('Date')
plt.ylabel('Ozone')
plt.title('Daily Airquality')
plt.show()
6. 라인 스타일 조정하기
1) color=
- 'red','green','blue' ...
- 혹은 'r', 'g', 'b', ...
2) linestyle=
- 'solid', 'dashed', 'dashdot', 'dotted
- 혹은 '-' | '--' | '-.' | ':’
3) marker =

plt.plot(data['Date'], data['Ozone’],
color='green’,
linestyle='dotted’,
marker='o')
plt.show()
7. 여러 그래프 겹치기
plt.plot(data['Date'], data['Ozone’]
, marker='o')
plt.plot(data['Date'], data['Temp’]
, marker='s')
plt.show()
1) 범례
- 각 plt.plot 함수 안에 label = 지정
- plt.legend() 추가
- 범례의 위치 : 가장 적절한데 표시
- 위치를 조절하려면(loc = ‘upper right’)
- best, upper right, upper left, lower left
2) 그리드
- plt.grid() 만 추가
plt.plot(data['Date'], data['Ozone’], label = 'Ozone')
plt.plot(data['Date'], data['Temp’], label = 'Temp')
plt.legend()
plt.grid()
plt.show()
3) 그래프 크기 조절
# 그래프 크기 조절 (가로, 세로)
# 가장 먼저 작성해야함
plt.figure(figsize = (12,8))
8. 데이터프레임.plot()
- 기본설정
- 기본적으로 제공
- xlabel, ylabel, xticks, legend 등
data.plot(x = 'Date', y = ['Temp','Ozone']
, title = 'Daily Airquality’)
plt.grid()
plt.show()
<Chapter6. 단변량 분석 - 숫자형>
1. 숫자형 변수를 정리하는 두가지 방법

1) 숫자로 요약하기: 정보의 대푯값 => 기초 통계량
- 평균(mean)
- 산술 평균 (arithmetic mean): 모든 값들을 더한 후, 개수로 나눈 수.
- 기하 평균 (geometric mean)
- 조화 평균 (harmonic mean): 분자가 동일한 두 비율의 평균
- 예 : 갈 때 90 km/h, 올 때 100 km/h 속력으로 왔으면, 평균 속력은? [a, b 역수]의 평균의 역수

# 넘파이 함수 이용하기
np.mean(titanic['Fare’])
# 판다스의 mean 메서드 이용하기
titanic['Fare'].mean()
⚠️ 평균(mean)을 대푯값으로 사용할 때 주의할 점
=> 정규분포나 비슷한 그래프의 형태가 아닌 이상 평균을 대표값으로 사용하지 않는게 좋음.
- 중위수(median)
- 자료의 순서상 가운데 위치한 값
# 넘파이 함수 이용하기
np.median(titanic['Fare’])
# 판다스의 median 메서드 이용하기
titanic['Fare'].median()
- 최빈값(mode)
- 자료 중에서 가장 빈번한 값
# 판다스의 mode 메서드 이용하기
titanic['Pclass'].mode()
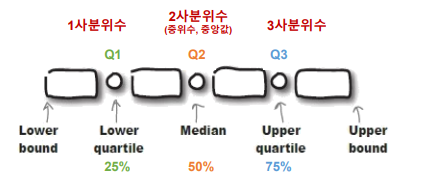
- 사분위수(Quantile)
- 데이터를 오름차순으로 정렬한 후,
- 전체를 4등분하고, 각 경계에 해당되는 값( 25%, 50%, 75%) 을 의미
2) 숫자로 요약하기: 기초 통계량
- 기초 총계량
- 숫자 몇 개로 분포를 요약
- df.describe()
- 기초 통계량
- count : 데이터 개수.
- Age의 개수가 다른 변수에 비해 적은 것은 NaN이 존재하기 때문
- 사분위수
- 25% : 1사분위수
- 50% : 2사분위수
- 75% : 3사분위수
- count : 데이터 개수.
- 기초 통계량
titanic.describe()
2.숫자형 변수 시각화하기
1) Histogram - 숫자형 변수 시각화
plt.hist(titanic.Fare, bins = 30, edgecolor = 'gray')
plt.xlabel('Fare')
plt.ylabel('Frequency')
plt.show()
- 히스토그램을 그릴 때, 주의 할 점 : bins를 적절히 조절
- 구간의 개수에 따라서 파악할 수 있는 내용이 달라짐.

plt.figure(figsize = (10, 10))
plt.subplot(2,2,1)
sns.histplot(x = 'Age' , data =titanic, bins = 8)
plt.subplot(2,2,2)
sns.histplot(x = 'Age' , data =titanic, bins = 16)
plt.subplot(2,2,3)
sns.histplot(x = 'Age' , data =titanic, bins = 32)
plt.subplot(2,2,4)
sns.histplot(x = 'Age' , data =titanic, bins = 64)
plt.show()
*️⃣ 그래프 읽기
1) 축의 의미 파악
2) 값이 분포로부터 파악할 내용
- 희박한 구간? 밀집 구간?
- 왜 그 구간은 희박한가?(밀집되어 있는가?) ➔ 이에 대한 비즈니스 의미 파악

2) Density Plot (KDE Plot)
- 히스토그램의 단점
- 구간(bin)의 너비를 어떻게 잡는지에 따라 전혀 다른 모양이 될 수 있음
- 밀도함수 그래프
- 막대의 너비를 가정하지 않고 모든 점에서 데이터의 밀도를 추정하는 커널 밀도 추정(Kernel Density Estimation)방식을 사용하여 이러한 단점을 해결.
- 밀도함수 그래프 아래 면적은
sns.kdeplot(titanic['Fare'])
# sns.kdeplot(x='Fare', data = titanic)
plt.show()
sns.histplot(x ='Age', data=titanic, bins= 16, kde=True)
plt.show()
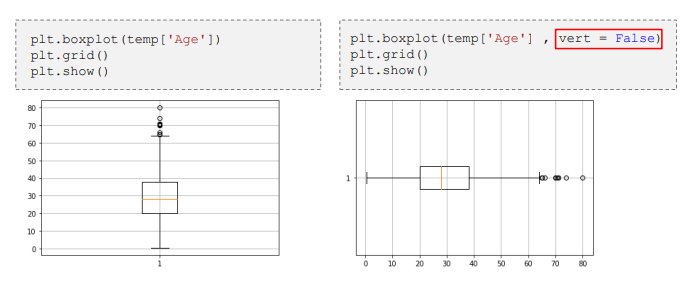
3) Box Plot - 숫자형 변수 시각화
- plt.boxplot()
- 사전에 반드시 NaN을 제외(sns.boxplot 은 NaN을 알아서 제거해 줌)
- vert 옵션 : 횡(False), 종(True, 기본값)



- IQR Inter Quartile Range
- 3사분위수 – 1사분위수

- Actual Whisker Length : 1.5*IQR 범위 이내의 최소, 최대값으로 결정
- Potential Whisker Length : 1.5*IQR 범위, 잠재적 수염의 길이 범위

<Chapter7. 단변량 분석 - 범주형 >
1. 범주형 변수
범주형 변수를 정리하는 방법 => 범주별 개수를 센다!
- 범주별 빈도수
- 범주별 비율
2. 범주형 변수 - 숫자로 요약
1) 범주별 빈도수
- 시리즈.value_counts()
titanic['Embarked'].value_counts()

2) 범주별 비율
- 시리즈.value_counts(normalize = True)
titanic['Embarked'].value_counts(normalize = True)
*️⃣ 해석
- 승객의 72.3%는 사우스햄튼에서 탑승
- 사우스햄튼, 퀸즈타운 : 2차산업혁명 중심도시 ➔ 미국에서 일자리를 구하기 위해 탑승
- 쉐부르 : 프랑스의 부촌 ➔ 관광 목적?
3. 범주형 변수 시각 : Bar Plot
1) sns.countplot
- 알아서 범주 별 빈도수가 계산되고 bar plot으로 그려짐.
sns.countplot(titanic['Pclass'])
plt.grid()
plt.show()
2) plt.bar
- 직접 범주 별 빈도수를 계산하고 그 결과를 입력해야 bar plot이 그려짐.
[2주차 02]